Lab 04: fitting probability distributions to your data using scipy.stats#
CCNY EAS 42000/A42000, Fall 2025, 2025/10/15, Prof. Spencer Hill
SUMMARY: We use xarray to load the netCDF file containing the Central Park weather station daily data from disk, and then a combination of xarray and scipy to fit parametric probability distributions to the data.
Preliminaries#
Imports#
from matplotlib import pyplot as plt # for plotting
import numpy as np # for working with arrays of numerical values
import scipy # for fitting PDFs
import xarray as xr # for loading data and subsequent analyses
Download the Central Park data if you don’t already have it#
# Modify this LOCAL_DATA_DIR as needed to point to where the dataset lives on your machine.
# It can be an *absolute path*, or a *relative path*, meaning relative to the
# directory that this notebook lives in.
# One dot, `.` means "the current directory." Two dots, `..` means "go up one directory."
LOCAL_DATA_DIR = "../data" # If you're in Colab: just ignore this.
!pip -q install pooch
import sys, pathlib, hashlib
import pooch
DATA_URL = (
"https://spencerahill.github.io/25f-stat-methods-course/_downloads/"
"91803b82950d49961a65355c075439b3/central-park-station-data_1869-01-01_2023-09-30.nc"
)
HASH_HEX = "85237a4bae1202030a36f330764fd5bd0c2c4fa484b3ae34a05db49fe7721eee"
DATA_DIR = pathlib.Path("/content/data" if "google.colab" in sys.modules else LOCAL_DATA_DIR)
DATA_DIR.mkdir(parents=True, exist_ok=True)
DATA_PATH = DATA_DIR / "central-park-station-data_1869-01-01_2023-09-30.nc"
def sha256sum(p: pathlib.Path) -> str:
return hashlib.sha256(p.read_bytes()).hexdigest()
need_fetch = (not DATA_PATH.exists()) or (sha256sum(DATA_PATH) != HASH_HEX)
if need_fetch:
fetched = pooch.retrieve(url=DATA_URL, known_hash=f"sha256:{HASH_HEX}",
path=DATA_DIR, fname=DATA_PATH.name)
print(f"Downloaded and verified: {fetched}")
else:
print(f"Verified existing file at {DATA_PATH}")
Verified existing file at ../data/central-park-station-data_1869-01-01_2023-09-30.nc
Load the Central Park data into an xarray.Dataset#
ds_cp = xr.open_dataset(DATA_PATH)
ds_cp
<xarray.Dataset> Size: 5MB
Dimensions: (time: 56520)
Coordinates:
* time (time) datetime64[ns] 452kB 1869-01-01 ... 2023-09-30
Data variables:
temp_max (time) int64 452kB ...
temp_min (time) int64 452kB ...
temp_avg (time) float64 452kB ...
temp_anom (time) float64 452kB ...
heat_deg_days (time) int64 452kB ...
cool_deg_days (time) int64 452kB ...
precip (time) float64 452kB ...
snow_fall (time) float64 452kB ...
snow_depth (time) int64 452kB ...Fit a PDF to the Central Park data using scipy.stats#
There are a ton of available distributions in scipy.stats. You can see a complete list along with other useful information on the associated docs page.
We can also see them, along with everything else defined within scipy.stats, using the built-in dir function:
dir(scipy.stats)
['Binomial',
'BootstrapMethod',
'CensoredData',
'ConstantInputWarning',
'Covariance',
'DegenerateDataWarning',
'FitError',
'Mixture',
'MonteCarloMethod',
'NearConstantInputWarning',
'Normal',
'PermutationMethod',
'Uniform',
'__all__',
'__builtins__',
'__cached__',
'__doc__',
'__file__',
'__loader__',
'__name__',
'__package__',
'__path__',
'__spec__',
'_ansari_swilk_statistics',
'_axis_nan_policy',
'_biasedurn',
'_binned_statistic',
'_binomtest',
'_bws_test',
'_censored_data',
'_common',
'_constants',
'_continuous_distns',
'_correlation',
'_covariance',
'_crosstab',
'_discrete_distns',
'_distn_infrastructure',
'_distr_params',
'_distribution_infrastructure',
'_entropy',
'_finite_differences',
'_fit',
'_hypotests',
'_kde',
'_ksstats',
'_levy_stable',
'_mannwhitneyu',
'_mgc',
'_morestats',
'_mstats_basic',
'_mstats_extras',
'_multicomp',
'_multivariate',
'_new_distributions',
'_odds_ratio',
'_page_trend_test',
'_probability_distribution',
'_qmc',
'_qmc_cy',
'_qmvnt',
'_qmvnt_cy',
'_quantile',
'_rcont',
'_relative_risk',
'_resampling',
'_sensitivity_analysis',
'_sobol',
'_stats',
'_stats_mstats_common',
'_stats_py',
'_stats_pythran',
'_survival',
'_tukeylambda_stats',
'_variation',
'_warnings_errors',
'_wilcoxon',
'abs',
'alexandergovern',
'alpha',
'anderson',
'anderson_ksamp',
'anglit',
'ansari',
'arcsine',
'argus',
'barnard_exact',
'bartlett',
'bayes_mvs',
'bernoulli',
'beta',
'betabinom',
'betanbinom',
'betaprime',
'biasedurn',
'binned_statistic',
'binned_statistic_2d',
'binned_statistic_dd',
'binom',
'binomtest',
'boltzmann',
'bootstrap',
'boschloo_exact',
'boxcox',
'boxcox_llf',
'boxcox_normmax',
'boxcox_normplot',
'bradford',
'brunnermunzel',
'burr',
'burr12',
'bws_test',
'cauchy',
'chatterjeexi',
'chi',
'chi2',
'chi2_contingency',
'chisquare',
'circmean',
'circstd',
'circvar',
'combine_pvalues',
'contingency',
'cosine',
'cramervonmises',
'cramervonmises_2samp',
'crystalball',
'cumfreq',
'describe',
'dgamma',
'differential_entropy',
'directional_stats',
'dirichlet',
'dirichlet_multinomial',
'distributions',
'dlaplace',
'dpareto_lognorm',
'dunnett',
'dweibull',
'ecdf',
'energy_distance',
'entropy',
'epps_singleton_2samp',
'erlang',
'exp',
'expectile',
'expon',
'exponnorm',
'exponpow',
'exponweib',
'f',
'f_oneway',
'false_discovery_control',
'fatiguelife',
'find_repeats',
'fisher_exact',
'fisk',
'fit',
'fligner',
'foldcauchy',
'foldnorm',
'friedmanchisquare',
'gamma',
'gausshyper',
'gaussian_kde',
'genexpon',
'genextreme',
'gengamma',
'genhalflogistic',
'genhyperbolic',
'geninvgauss',
'genlogistic',
'gennorm',
'genpareto',
'geom',
'gibrat',
'gmean',
'gompertz',
'goodness_of_fit',
'gstd',
'gumbel_l',
'gumbel_r',
'gzscore',
'halfcauchy',
'halfgennorm',
'halflogistic',
'halfnorm',
'hmean',
'hypergeom',
'hypsecant',
'invgamma',
'invgauss',
'invweibull',
'invwishart',
'iqr',
'irwinhall',
'jarque_bera',
'jf_skew_t',
'johnsonsb',
'johnsonsu',
'kappa3',
'kappa4',
'kde',
'kendalltau',
'kruskal',
'ks_1samp',
'ks_2samp',
'ksone',
'kstat',
'kstatvar',
'kstest',
'kstwo',
'kstwobign',
'kurtosis',
'kurtosistest',
'landau',
'laplace',
'laplace_asymmetric',
'levene',
'levy',
'levy_l',
'levy_stable',
'linregress',
'lmoment',
'log',
'loggamma',
'logistic',
'loglaplace',
'lognorm',
'logrank',
'logser',
'loguniform',
'lomax',
'make_distribution',
'mannwhitneyu',
'matrix_normal',
'maxwell',
'median_abs_deviation',
'median_test',
'mielke',
'mode',
'moment',
'monte_carlo_test',
'mood',
'morestats',
'moyal',
'mstats',
'mstats_basic',
'mstats_extras',
'multinomial',
'multiscale_graphcorr',
'multivariate_hypergeom',
'multivariate_normal',
'multivariate_t',
'mvn',
'mvsdist',
'nakagami',
'nbinom',
'ncf',
'nchypergeom_fisher',
'nchypergeom_wallenius',
'nct',
'ncx2',
'nhypergeom',
'norm',
'normal_inverse_gamma',
'normaltest',
'norminvgauss',
'obrientransform',
'order_statistic',
'ortho_group',
'page_trend_test',
'pareto',
'pearson3',
'pearsonr',
'percentileofscore',
'permutation_test',
'planck',
'pmean',
'pointbiserialr',
'poisson',
'poisson_binom',
'poisson_means_test',
'power',
'power_divergence',
'powerlaw',
'powerlognorm',
'powernorm',
'ppcc_max',
'ppcc_plot',
'probplot',
'qmc',
'quantile',
'quantile_test',
'randint',
'random_correlation',
'random_table',
'rankdata',
'ranksums',
'rayleigh',
'rdist',
'recipinvgauss',
'reciprocal',
'rel_breitwigner',
'relfreq',
'rice',
'rv_continuous',
'rv_discrete',
'rv_histogram',
'scoreatpercentile',
'sem',
'semicircular',
'shapiro',
'siegelslopes',
'sigmaclip',
'skellam',
'skew',
'skewcauchy',
'skewnorm',
'skewtest',
'sobol_indices',
'somersd',
'spearmanr',
'special_ortho_group',
'stats',
'studentized_range',
't',
'test',
'theilslopes',
'tiecorrect',
'tmax',
'tmean',
'tmin',
'trapezoid',
'triang',
'trim1',
'trim_mean',
'trimboth',
'truncate',
'truncexpon',
'truncnorm',
'truncpareto',
'truncweibull_min',
'tsem',
'tstd',
'ttest_1samp',
'ttest_ind',
'ttest_ind_from_stats',
'ttest_rel',
'tukey_hsd',
'tukeylambda',
'tvar',
'uniform',
'uniform_direction',
'unitary_group',
'variation',
'vonmises',
'vonmises_fisher',
'vonmises_line',
'wald',
'wasserstein_distance',
'wasserstein_distance_nd',
'weibull_max',
'weibull_min',
'weightedtau',
'wilcoxon',
'wishart',
'wrapcauchy',
'yeojohnson',
'yeojohnson_llf',
'yeojohnson_normmax',
'yeojohnson_normplot',
'yulesimon',
'zipf',
'zipfian',
'zmap',
'zscore']
To start, let’s use the normal function, which is scipy.stats.norm:
help(scipy.stats.norm)
Help on norm_gen in module scipy.stats._continuous_distns:
<scipy.stats._continuous_distns.norm_gen object>
A normal continuous random variable.
The location (``loc``) keyword specifies the mean.
The scale (``scale``) keyword specifies the standard deviation.
As an instance of the `rv_continuous` class, `norm` object inherits from it
a collection of generic methods (see below for the full list),
and completes them with details specific for this particular distribution.
Methods
-------
rvs(loc=0, scale=1, size=1, random_state=None)
Random variates.
pdf(x, loc=0, scale=1)
Probability density function.
logpdf(x, loc=0, scale=1)
Log of the probability density function.
cdf(x, loc=0, scale=1)
Cumulative distribution function.
logcdf(x, loc=0, scale=1)
Log of the cumulative distribution function.
sf(x, loc=0, scale=1)
Survival function (also defined as ``1 - cdf``, but `sf` is sometimes more accurate).
logsf(x, loc=0, scale=1)
Log of the survival function.
ppf(q, loc=0, scale=1)
Percent point function (inverse of ``cdf`` --- percentiles).
isf(q, loc=0, scale=1)
Inverse survival function (inverse of ``sf``).
moment(order, loc=0, scale=1)
Non-central moment of the specified order.
stats(loc=0, scale=1, moments='mv')
Mean('m'), variance('v'), skew('s'), and/or kurtosis('k').
entropy(loc=0, scale=1)
(Differential) entropy of the RV.
fit(data)
Parameter estimates for generic data.
See `scipy.stats.rv_continuous.fit <https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.rv_continuous.fit.html#scipy.stats.rv_continuous.fit>`__ for detailed documentation of the
keyword arguments.
expect(func, args=(), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)
Expected value of a function (of one argument) with respect to the distribution.
median(loc=0, scale=1)
Median of the distribution.
mean(loc=0, scale=1)
Mean of the distribution.
var(loc=0, scale=1)
Variance of the distribution.
std(loc=0, scale=1)
Standard deviation of the distribution.
interval(confidence, loc=0, scale=1)
Confidence interval with equal areas around the median.
Notes
-----
The probability density function for `norm` is:
.. math::
f(x) = \frac{\exp(-x^2/2)}{\sqrt{2\pi}}
for a real number :math:`x`.
The probability density above is defined in the "standardized" form. To shift
and/or scale the distribution use the ``loc`` and ``scale`` parameters.
Specifically, ``norm.pdf(x, loc, scale)`` is identically
equivalent to ``norm.pdf(y) / scale`` with
``y = (x - loc) / scale``. Note that shifting the location of a distribution
does not make it a "noncentral" distribution; noncentral generalizations of
some distributions are available in separate classes.
Examples
--------
>>> import numpy as np
>>> from scipy.stats import norm
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)
Get the support:
>>> lb, ub = norm.support()
Calculate the first four moments:
>>> mean, var, skew, kurt = norm.stats(moments='mvsk')
Display the probability density function (``pdf``):
>>> x = np.linspace(norm.ppf(0.01),
... norm.ppf(0.99), 100)
>>> ax.plot(x, norm.pdf(x),
... 'r-', lw=5, alpha=0.6, label='norm pdf')
Alternatively, the distribution object can be called (as a function)
to fix the shape, location and scale parameters. This returns a "frozen"
RV object holding the given parameters fixed.
Freeze the distribution and display the frozen ``pdf``:
>>> rv = norm()
>>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')
Check accuracy of ``cdf`` and ``ppf``:
>>> vals = norm.ppf([0.001, 0.5, 0.999])
>>> np.allclose([0.001, 0.5, 0.999], norm.cdf(vals))
True
Generate random numbers:
>>> r = norm.rvs(size=1000)
And compare the histogram:
>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2)
>>> ax.set_xlim([x[0], x[-1]])
>>> ax.legend(loc='best', frameon=False)
>>> plt.show()
Let’s start with daily minimum temperatures in the month of May:
temp_min_may = ds_cp["temp_min"].where(ds_cp["time"].dt.month == 5, drop=True)
First let’s plot it’s histogram:
temp_min_may.plot.hist(density=True)
(array([0.00021907, 0. , 0. , 0. , 0.00052029,
0.01377403, 0.05561641, 0.0423079 , 0.01659456, 0.00254669]),
array([ 0. , 7.6, 15.2, 22.8, 30.4, 38. , 45.6, 53.2, 60.8, 68.4, 76. ]),
<BarContainer object of 10 artists>)
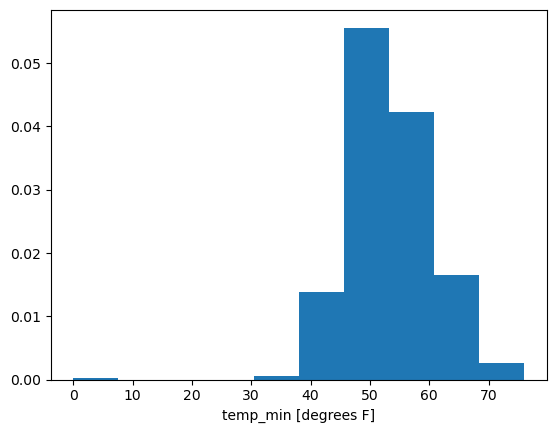
We see here the spurious 0 values. So let’s drop those:
temp_min_may = temp_min_may.where(temp_min_may > 0, drop=True)
Now we can try the histogram again:
temp_min_may.plot.hist(density=True, bins=15)
(array([0.00028427, 0.00106601, 0.00369549, 0.01435556, 0.02949286,
0.04704645, 0.06346296, 0.06140201, 0.04740179, 0.03176701,
0.02025414, 0.01179715, 0.00575644, 0.00248735, 0.0006396 ]),
array([32. , 34.93333333, 37.86666667, 40.8 , 43.73333333,
46.66666667, 49.6 , 52.53333333, 55.46666667, 58.4 ,
61.33333333, 64.26666667, 67.2 , 70.13333333, 73.06666667,
76. ]),
<BarContainer object of 15 artists>)
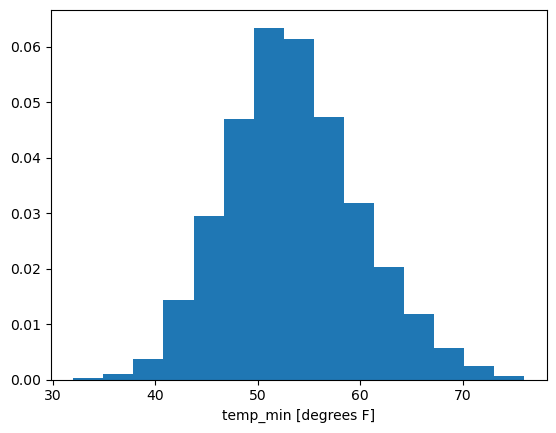
That looks pretty normal—as in, pretty Gaussian—to me!
So let’s proceed with fitting a normal distribution to the data.
To do so we use the .fit method of scipy.stats.norm. You simply give it the data you want to fit as the sole argument, and it returns the best-fit values of both of the normal distribution’s parameters: the mean \(\mu\) and standard deviation \(\sigma\).
mean, stdev = scipy.stats.norm.fit(temp_min_may)
mean, stdev
(np.float64(53.42172190952679), np.float64(6.63132999778397))
This means that the best-fit normal distribution for this data has a mean near 53.4\(^\circ\)F and a standard deviation near 6.6\(^\circ\)F
Now let’s overlay this on the histogram to inspect by eye how well it performs.
First, we’ll create a “frozen” normal PDF by specifying these values of the mean and standard deviation in a new call to scipy.stats.norm.
Note: the mean is called loc, and the standard deviation is called scale, because these are shared names across all distributions…different distributions have different parameters and names for them, and so scipy uses these “universal” names of loc and scale (along with others).
normal_for_tmin_may = scipy.stats.norm(loc=mean, scale=stdev)
normal_for_tmin_may
<scipy.stats._distn_infrastructure.rv_continuous_frozen at 0x7f16d1d96510>
Now we can call this object’s pdf method, giving it any point or points we want to know the PDF value at:
print(normal_for_tmin_may.pdf(50)) # the value of this PDF at 50 deg F
print(normal_for_tmin_may.pdf([40, 100])) # the PDF's value at the two points 40 deg F and 100 deg F
0.05266161442811993
[7.75820374e-03 1.16437434e-12]
What we want to do is visually inspect how this PDF compares to our histogram above across the whole range of values.
To do that, we’ll compute the PDF at a whole bunch of individual values spanning that range, and then plot the line connecting all those individual values.
To do so, we’ll create the array of x values over which the values of this distribution’s PDF will be plotted.
To do this we’ll make use of numpy’s linspace function, which creates an array of equally spaced points between two specified endpoints:
help(np.linspace)
Help on _ArrayFunctionDispatcher in module numpy:
linspace(
start,
stop,
num=50,
endpoint=True,
retstep=False,
dtype=None,
axis=0,
*,
device=None
)
Return evenly spaced numbers over a specified interval.
Returns `num` evenly spaced samples, calculated over the
interval [`start`, `stop`].
The endpoint of the interval can optionally be excluded.
.. versionchanged:: 1.20.0
Values are rounded towards ``-inf`` instead of ``0`` when an
integer ``dtype`` is specified. The old behavior can
still be obtained with ``np.linspace(start, stop, num).astype(int)``
Parameters
----------
start : array_like
The starting value of the sequence.
stop : array_like
The end value of the sequence, unless `endpoint` is set to False.
In that case, the sequence consists of all but the last of ``num + 1``
evenly spaced samples, so that `stop` is excluded. Note that the step
size changes when `endpoint` is False.
num : int, optional
Number of samples to generate. Default is 50. Must be non-negative.
endpoint : bool, optional
If True, `stop` is the last sample. Otherwise, it is not included.
Default is True.
retstep : bool, optional
If True, return (`samples`, `step`), where `step` is the spacing
between samples.
dtype : dtype, optional
The type of the output array. If `dtype` is not given, the data type
is inferred from `start` and `stop`. The inferred dtype will never be
an integer; `float` is chosen even if the arguments would produce an
array of integers.
axis : int, optional
The axis in the result to store the samples. Relevant only if start
or stop are array-like. By default (0), the samples will be along a
new axis inserted at the beginning. Use -1 to get an axis at the end.
device : str, optional
The device on which to place the created array. Default: None.
For Array-API interoperability only, so must be ``"cpu"`` if passed.
.. versionadded:: 2.0.0
Returns
-------
samples : ndarray
There are `num` equally spaced samples in the closed interval
``[start, stop]`` or the half-open interval ``[start, stop)``
(depending on whether `endpoint` is True or False).
step : float, optional
Only returned if `retstep` is True
Size of spacing between samples.
See Also
--------
arange : Similar to `linspace`, but uses a step size (instead of the
number of samples).
geomspace : Similar to `linspace`, but with numbers spaced evenly on a log
scale (a geometric progression).
logspace : Similar to `geomspace`, but with the end points specified as
logarithms.
:ref:`how-to-partition`
Examples
--------
>>> import numpy as np
>>> np.linspace(2.0, 3.0, num=5)
array([2. , 2.25, 2.5 , 2.75, 3. ])
>>> np.linspace(2.0, 3.0, num=5, endpoint=False)
array([2. , 2.2, 2.4, 2.6, 2.8])
>>> np.linspace(2.0, 3.0, num=5, retstep=True)
(array([2. , 2.25, 2.5 , 2.75, 3. ]), 0.25)
Graphical illustration:
>>> import matplotlib.pyplot as plt
>>> N = 8
>>> y = np.zeros(N)
>>> x1 = np.linspace(0, 10, N, endpoint=True)
>>> x2 = np.linspace(0, 10, N, endpoint=False)
>>> plt.plot(x1, y, 'o')
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.plot(x2, y + 0.5, 'o')
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.ylim([-0.5, 1])
(-0.5, 1)
>>> plt.show()
xvals_for_norm_fit = np.linspace(temp_min_may.min().values, temp_min_may.max().values, 100)
xvals_for_norm_fit
array([32. , 32.44444444, 32.88888889, 33.33333333, 33.77777778,
34.22222222, 34.66666667, 35.11111111, 35.55555556, 36. ,
36.44444444, 36.88888889, 37.33333333, 37.77777778, 38.22222222,
38.66666667, 39.11111111, 39.55555556, 40. , 40.44444444,
40.88888889, 41.33333333, 41.77777778, 42.22222222, 42.66666667,
43.11111111, 43.55555556, 44. , 44.44444444, 44.88888889,
45.33333333, 45.77777778, 46.22222222, 46.66666667, 47.11111111,
47.55555556, 48. , 48.44444444, 48.88888889, 49.33333333,
49.77777778, 50.22222222, 50.66666667, 51.11111111, 51.55555556,
52. , 52.44444444, 52.88888889, 53.33333333, 53.77777778,
54.22222222, 54.66666667, 55.11111111, 55.55555556, 56. ,
56.44444444, 56.88888889, 57.33333333, 57.77777778, 58.22222222,
58.66666667, 59.11111111, 59.55555556, 60. , 60.44444444,
60.88888889, 61.33333333, 61.77777778, 62.22222222, 62.66666667,
63.11111111, 63.55555556, 64. , 64.44444444, 64.88888889,
65.33333333, 65.77777778, 66.22222222, 66.66666667, 67.11111111,
67.55555556, 68. , 68.44444444, 68.88888889, 69.33333333,
69.77777778, 70.22222222, 70.66666667, 71.11111111, 71.55555556,
72. , 72.44444444, 72.88888889, 73.33333333, 73.77777778,
74.22222222, 74.66666667, 75.11111111, 75.55555556, 76. ])
fig, ax = plt.subplots()
temp_min_may.plot.hist(ax=ax, density=True, bins=15)
plt.plot(xvals_for_norm_fit, normal_for_tmin_may.pdf(xvals_for_norm_fit))
[<matplotlib.lines.Line2D at 0x7f16d1caad50>]
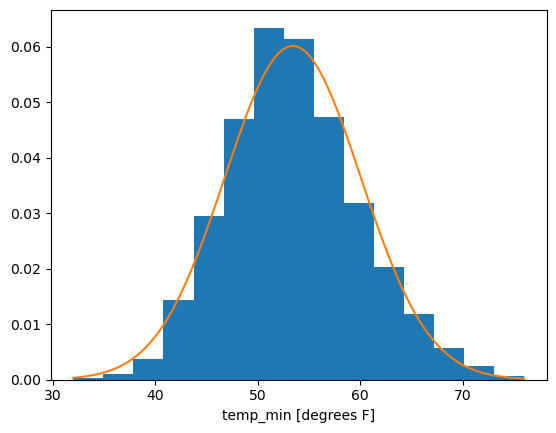
Nice! By visual inspection, this sample of daily minimum temperatures in the month of May for 1869-2023 looks pretty well approximated by a normal distribution!